KörperDefinition Körper
Der Begriff Körper bezeichnet mehrere Dinge
- algebraischer Körper: Eine Menge mit Verknüpfungen zwischen den Elementen
- geometrischer Körper: Ein von Flächen begrenztes Objekt
geometrischer Körper
Ein von (ebenen oder gekrümmten) Flächen begrenztes Objekt, das ein Volumen und eine Oberfläche hat.
Spezielle geometrische Körper
Kegel
Kugel
Polyeder: Ein Körper, der nur von ebenen Flächen begrenzt wird
Prisma: Ein Polyeder
Pyramide
Tetraeder: Ein Polyeder
Quader: Ein Polyeder
Würfel: Ein Polyeder
Zylinder
algebraischer Körper
Eine Menge K zusammen mit zwei Verknüpfungen 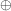 und und 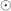 heißt Körper, wenn folgende Bedingungen erfüllt sind: heißt Körper, wenn folgende Bedingungen erfüllt sind:
I.) 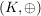 ist eine abelsche (=kommutative) Gruppe. ist eine abelsche (=kommutative) Gruppe.
Das neutrale Element sei mit "0" bezeichnet.
II.) 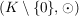 ist eine Gruppe. ist eine Gruppe.
Das neutrale Element sei mit "1" bezeichnet.
III.) Es gelten die Distributivgesetze: 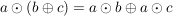 und und 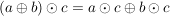 für alle für alle 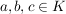 . .
Gilt zusätzlich für die Verknüpfung 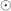 das Kommutativgesetz, so heißt der Körper kommutativer Körper. Häufig wird aber auch unter einem Körper ein kommutativen Körper verstanden, im Zweifel ist in der jeweiligen Quelle nachzuschlagen. das Kommutativgesetz, so heißt der Körper kommutativer Körper. Häufig wird aber auch unter einem Körper ein kommutativen Körper verstanden, im Zweifel ist in der jeweiligen Quelle nachzuschlagen.
Nichtkommutative Körper heißen auch Schiefkörper oder Divisionsalgebren oder Divisionsbereich.
siehe auch für Schüler zum Nachlesen:
http://www.hausarbeiten.de/faecher/vorschau/109361.html
http://www.mathepedia.de/Ringe_und_Koerper.aspx
Eigenschaften spezieller Körper
;angeordneter Körper / geordneter Körper
Ein Körper K mit einer totalen Ordnung für den zusätzlich für alle 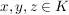 die Bedingungen die Bedingungen
IV.) 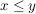 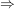 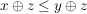 (Monotonie der Addition) (Monotonie der Addition)
V.) 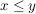 und und 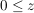 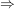 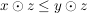 (Monotonie der Multiplikation) (Monotonie der Multiplikation)
gelten, heißt angeordneter Körper.
Quellen: (1)
;archimedisch angeordneter Körper
VI.) Ein angeordneter Körper K, bei dem die Folge der Vielfachen von 1 (="neutrales Element der Multiplikation") unbeschränkt ist, heißt archimedisch angeordneter Körper.
Quellen: (1)
;kommutativer Körper
;nullteilerfreier Körper
Beispiele.
Kommutative Körper: 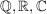 oder die endlichen Körper oder die endlichen Körper 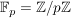 (p prim). (p prim).
Quellen
(1) isbn3411032049
|