WinkelfunktionDefinition Sinus(-funktion), Kosinus(-funktion), Tangens(-funktion)
Schule
Betrachtet man das unten stehende rechtwinklige Dreieck ABC mit dem rechten Winkel bei C (Bild1),
so gelten folgende Beziehungen:
Dabei ist die Strecke 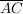 die Ankathete zum Winkel die Ankathete zum Winkel 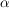
und die Strecke 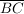 die Gegenkathete zum Winkel die Gegenkathete zum Winkel 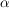 . .
Definition am Einheitskreis
Mit Hilfe des Satzes des Pythagoras gilt: 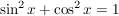 , weil im Einheitskreis die Hypotenuse c = r = 1 ist. , weil im Einheitskreis die Hypotenuse c = r = 1 ist.
Man kann diese Definition am rechtwinkligen Dreieck auf Winkel >90° erweitern, wenn man folgendes Bild2 betrachtet:
Durchläuft der Punkt C die Kreislinie, so kann man die zum Winkel 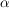 (bei A) gehörenden Werte des Sinus (bei A) gehörenden Werte des Sinus 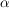 und Kosinus und Kosinus 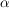 in ein Koordinatenkreuz übertragen. in ein Koordinatenkreuz übertragen.
Sinusfunktion:
Kosinusfunktion:
Man erkennt, dass sowohl der Sinus als auch der Kosinus stets Werte 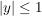 ergeben. ergeben.
In den Zeichnungen sind die Winkel im Bogenmaß aufgetragen;
dabei gelten folgende Entsprechungen mit  = Kreiszahl = 3.1415926...: = Kreiszahl = 3.1415926...:
Man erkennt weiter, dass sich nach einer Umdrehung (gegen den Uhrzeigersinn) die Werte für den Sinus und den Kosinus wiederholen: beide Funktionen sind periodisch mit der Periodenlänge  . .
Daher kann man die Sinus- und die Kosinusfunktion auch für Werte > 90° sinnvoll definieren.
Natürlich kann man den Punkt C auch mit dem Uhrzeiger auf dem Kreis wandern lassen:
dann bezeichnet man einfach die entstehenden Winkel als negative Größen.
Damit ist also festgestellt, dass der Definitionsbereich beider Funktionen ganz 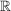 ist. ist.
weitere Eigenschaften der Winkelfunktionen
Universität
Definition/Darstellung als Potenzreihe
Für 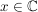 (insbesondere für (insbesondere für  ) ist definiert (Taylorreihe des Sinus): ) ist definiert (Taylorreihe des Sinus):
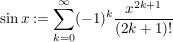
Für 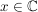 (insbesondere für (insbesondere für  ) ist definiert (Taylorreihe des Kosinus): ) ist definiert (Taylorreihe des Kosinus):

Weitere Beziehungen
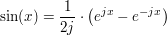
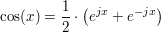
Bild1 Rechtwinkliges Dreieck aus ![Link auf "http://de.wikipedia.org/wiki/Sinus" [link]](/images/popup.gif) Wikipedia Wikipedia
weitere Überlegungen zur Tangensfunktion
|