Ordnung eines Gruppenelements
!!Definition ''Ordnung eines Gruppenelements'
Universität
Die Ordnung der von einem Element  einer Gruppe einer Gruppe 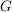 erzeugten zyklischen Untergruppe erzeugten zyklischen Untergruppe 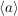 heißt die Ordnung von heißt die Ordnung von  . Sie wird oft mit . Sie wird oft mit  bezeichnet: bezeichnet:
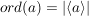 . .
Zum Beispiel hat jedes Element in 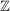 eine unendliche Ordnung, hingegen gilt: eine unendliche Ordnung, hingegen gilt:
 für für 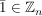 . .
Betrachtet man eine zyklische Untergruppe 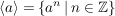 für ein Element für ein Element  einer Gruppe einer Gruppe 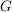 , dann sind entweder sämtliche Potenzen von , dann sind entweder sämtliche Potenzen von  verschieden und verschieden und  hat unendliche Ordnung, oder es gibt hat unendliche Ordnung, oder es gibt 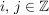 , , 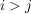 mit mit 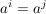 . Hieraus folgt: . Hieraus folgt:
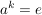 für für 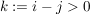 , ,
d.h. es gibt eine natürliche Zahl 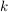 mit mit 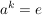 . Es sei . Es sei  die kleinste positive Zahl mit die kleinste positive Zahl mit 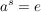 . Dann sind in . Dann sind in 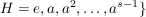 alle Elemente voneinander verschieden (wegen der Minimalität von alle Elemente voneinander verschieden (wegen der Minimalität von  ). Wegen ). Wegen 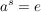 ist ist 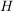 multipilkativ abgeschlossen, d.h. es gilt: multipilkativ abgeschlossen, d.h. es gilt: 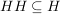 . Da . Da 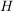 endlich ist, folgt daraus bereits, dass endlich ist, folgt daraus bereits, dass 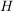 eine Untergruppe von eine Untergruppe von 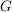 ist. Man hat zudem ist. Man hat zudem 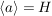 . .
Es folgt:
Die Ordnung von 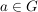 ist unendlich oder gleich der kleinsten positiven Zahl ist unendlich oder gleich der kleinsten positiven Zahl  mit mit 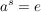 . Hat . Hat 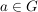 die (endliche) Ordnung die (endliche) Ordnung  , dann ist , dann ist
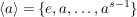 . .
Es gilt in diesem endlichen Fall 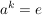 genau dann, wenn genau dann, wenn 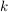 ein Vielfaches von ein Vielfaches von  ist, also ist, also 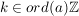 . .
Für alle 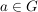 mit mit 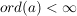 und alle und alle 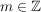 gilt: gilt:
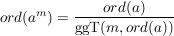 . .
Quelle: isbn3446130799
|