StabilitätStabilität von Regelkreisen
Regelkreise können aufgrund der Rückführungsstruktur instabil werden. Es treten dann Schwingungen auf, deren Amplituden über alle Grenzen anwachsen und das System zerstören.
Ein lineares zeitinvariantes Übertragungssystem heißt
stabil: wenn 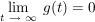 , d.h. die Gewichtsfunktion asymptotisch auf Null abklingt.
grenzstabil: wenn 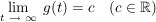 , d.h. die Gewichtsfunktion asymptotisch einem endlichen Grenzwert zustrebt.
instabil: wenn 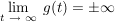 , d.h. die Gewichtsfunktion betragsmäßig gegen unendlich geht.
Die Stabilität ist daher eine Systemeigenschaft
zur Übersicht "Regelungstechnik"
| 
