innerer Automorphismus
!!Definition ''innerer Automorphismus"
Universität
Es sei 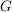 eine Gruppe und eine Gruppe und 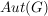 ihre Automorphismengruppe. ihre Automorphismengruppe.
Für jedes 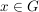 kann man einen Automorphismus kann man einen Automorphismus 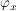 wie folgt angeben: wie folgt angeben:
![$ \varphi_x : \begin{array}{ccc} G & \to & G \\[5pt] y & \mapsto & \varphi_x(y):=xyx^{-1} \end{array} $ $ \varphi_x : \begin{array}{ccc} G & \to & G \\[5pt] y & \mapsto & \varphi_x(y):=xyx^{-1} \end{array} $](/teximg/5/0/00392105.png) . .
Wegen
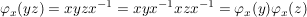
ist 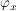 ein Homomorphismus. Aus ein Homomorphismus. Aus
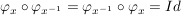
ersieht man, dass 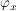 sogar ein Automorphismus ist. sogar ein Automorphismus ist.
Ein Element 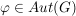 heißt ein innerer Automorphimus, wenn es ein heißt ein innerer Automorphimus, wenn es ein 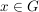 gibt mit gibt mit 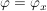 . .
Elemente 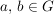 heißen konjugiert, wenn es ein heißen konjugiert, wenn es ein 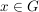 gibt mit gibt mit
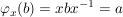 . .
Siehe auch: Zentrum
Quelle: isbn3446130799
|